有以下三个命题：
①在平面内, 设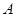
、
为两个定点,
为动点,且
,其中常数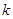
为正实数，则动点的轨迹为双曲线；
②已知△ABC的周长为20，且顶点B (0，-4)，C (0，4)，则顶点A的轨迹方程是
；
③双曲线
与椭圆
有相同的焦点.
其中是真命题的序号为 .（写出所有真命题的序号）
.
过焦点的弦为直径的圆截y轴所得的弦长为4, 该圆的方程是 
则
__.
是虚数单位，
则
.相关知识点
推荐套卷
有以下三个命题：
①在平面内, 设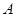、为两个定点,为动点,且,其中常数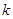为正实数，则动点的轨迹为双曲线；
②已知△ABC的周长为20，且顶点B (0，-4)，C (0，4)，则顶点A的轨迹方程是；
③双曲线与椭圆有相同的焦点.
其中是真命题的序号为 .（写出所有真命题的序号）
粤公网安备 44130202000953号