（本小题满分10分）选修4-4：坐标系与参数方程
已知极坐标系的极点在直角坐标系的原点处，极轴与
轴的正半轴重合，曲线C1 
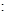
（t为参数），曲线
．
（Ⅰ）写出C1与C2的普通方程；
（Ⅱ）过坐标原点O做C1的垂线，垂足为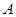
，P为OA中点，当
变化时，求P点的轨迹的参数方程，并指出它是什么曲线．
相关试题
通过点P（1,1），且在点Q（2，-1）处与直线y=x-3相切，求实数a,b,c的值。
有共同的渐近线，并且经过点
的双曲线方程．
的首项
，且
，
；
是否为等比数列，并证明你的结论．
的通项公式.
中，内角
对边的边长分别是
，已知
，
．
，求
；
，求
求a，b的值；推荐套卷
（本小题满分10分）选修4-4：坐标系与参数方程
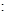
已知极坐标系的极点在直角坐标系的原点处，极轴与轴的正半轴重合，曲线C1 （t为参数），曲线．
（Ⅰ）写出C1与C2的普通方程；
（Ⅱ）过坐标原点O做C1的垂线，垂足为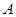，P为OA中点，当变化时，求P点的轨迹的参数方程，并指出它是什么曲线．
粤公网安备 44130202000953号