（本小题满分12分）如图所示，直角梯形ACDE与等腰直角△ABC所在平面互相垂直，F为BC的中点，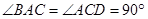
，AE∥C
D，DC=AC=2AE=2.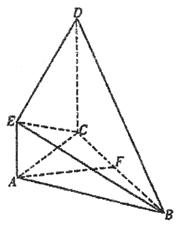
（Ⅰ）求证：平面BCD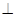
平面ABC
（Ⅱ）求证：AF∥平面BDE；
（Ⅲ）求四面体B-CDE的体积.
的定义域；
为何值时，函数值大于1.
在
上具有单调性，求实数k的取值范围。
，
的图象；
（2）
（2）
推荐套卷
（本小题满分12分）如图所示，直角梯形ACDE与等腰直角△ABC所在平面互相垂直，F为BC的中点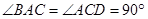，，AE∥CD，DC=AC=2AE=2.
（Ⅰ）求证：平面BCD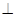平面ABC
（Ⅱ）求证：AF∥平面BDE；
（Ⅲ）求四面体B-CDE的体积.
粤公网安备 44130202000953号