.已知直线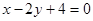
经过椭圆
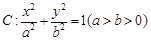的左顶点A和上顶点D，椭圆C的右顶点为B，点P是椭圆C上位于
轴上方的动点，直线AP，BP与直线
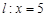分别交于M，N两点.
(1)求椭圆C的方程；
(2)求线段MN的长度的最小值；
(3)当线段MN的长度最小时，Q点在椭圆上运动，记△BPQ的面积为S，当S在
上变化时，讨论S的大小与Q点的个数之间的关系.
中，角
所对的边分别为
,设
为
.
的大小；
的最大值.
的焦点
和
，长轴长6，设直线
交椭圆
，
两点，求线段
的中点坐标.
，对于任意的
，均有
成立，求实数
的取值范围
是虚数，
是实数，且
，求
的值及
，当实数
取什么值时，复数
是推荐套卷
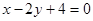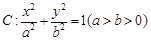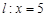.已知直线经过椭圆的左顶点A和上顶点D，椭圆C的右顶点为B，点P是椭圆C上位于轴上方的动点，直线AP，BP与直线分别交于M，N两点.
(1)求椭圆C的方程；
(2)求线段MN的长度的最小值；
(3)当线段MN的长度最小时，Q点在椭圆上运动，记△BPQ的面积为S，当S在上变化时，讨论S的大小与Q点的个数之间的关系.
粤公网安备 44130202000953号