如图(1),凸四边形 ,如果点
,如果点 满足
满足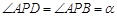 ,且
,且 ,则称点
,则称点 为四边形
为四边形 的一个半等角点.
的一个半等角点.在图(2)正方形
 内画一个半等角点
内画一个半等角点 ,且满足
,且满足 ;
;在图(3)四边形
 中画出一个半等角点
中画出一个半等角点 ,
,
保留画图痕迹(不需写出画法).

相关知识点
推荐套卷
如图(1),凸四边形 ,如果点
,如果点 满足
满足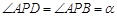 ,且
,且 ,则称点
,则称点 为四边形
为四边形 的一个半等角点.
的一个半等角点.在图(2)正方形
 内画一个半等角点
内画一个半等角点 ,且满足
,且满足 ;
;在图(3)四边形
 中画出一个半等角点
中画出一个半等角点 ,
,
保留画图痕迹(不需写出画法).
