经过原点和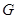 (4,0)的两条抛物线
(4,0)的两条抛物线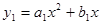 ,
,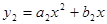 ,顶点分别为
,顶点分别为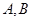 ,且都在第1象限,连结
,且都在第1象限,连结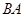 交
交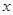 轴于
轴于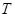 ,且
,且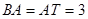 .
.分别求出抛物线
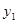 和
和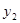 的解析式;
的解析式;点C是抛物线
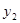 的
的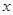 轴上方的一动点,作
轴上方的一动点,作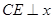 轴于
轴于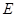 ,交抛物线
,交抛物线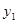 于D,试判断
于D,试判断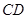 和
和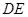 的数量关系,并说明理由;
的数量关系,并说明理由;直线
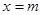 ,交抛物线
,交抛物线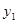 于M,交抛物线
于M,交抛物线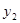 于N,是否存在以点
于N,是否存在以点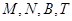 为顶点的四边形是平行四边形,若存在,求出
为顶点的四边形是平行四边形,若存在,求出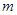 的值;若不存在,说明理由..
的值;若不存在,说明理由..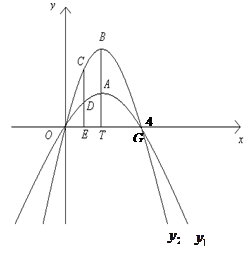
相关知识点
推荐套卷
经过原点和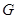 (4,0)的两条抛物线
(4,0)的两条抛物线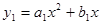 ,
,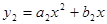 ,顶点分别为
,顶点分别为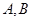 ,且都在第1象限,连结
,且都在第1象限,连结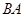 交
交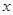 轴于
轴于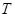 ,且
,且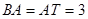 .
.分别求出抛物线
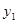 和
和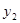 的解析式;
的解析式;点C是抛物线
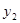 的
的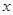 轴上方的一动点,作
轴上方的一动点,作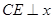 轴于
轴于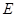 ,交抛物线
,交抛物线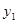 于D,试判断
于D,试判断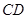 和
和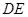 的数量关系,并说明理由;
的数量关系,并说明理由;直线
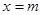 ,交抛物线
,交抛物线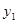 于M,交抛物线
于M,交抛物线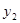 于N,是否存在以点
于N,是否存在以点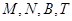 为顶点的四边形是平行四边形,若存在,求出
为顶点的四边形是平行四边形,若存在,求出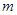 的值;若不存在,说明理由..
的值;若不存在,说明理由..