综合与探究:如图,抛物线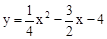 与x轴交于A,B两点(点B在点A的右侧)与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q。
与x轴交于A,B两点(点B在点A的右侧)与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q。
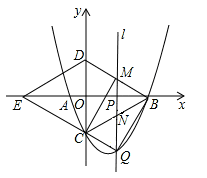
(1)求点A,B,C的坐标。
(2)当点P在线段OB上运动时,直线l分别交BD,BC于点M,N。试探究m为何值时,四边形CQMD是平行四边形,此时,请判断四边形CQBM的形状,并说明理由。
(3)当点P在线段EB上运动时,是否存在点 Q,使△BDQ为直角三角形,若存在,请直接写出点Q的坐标;若不存在,请说明理由。