(长为3的线段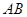 的两个端点
的两个端点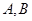 分别在
分别在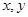 轴上移动,点
轴上移动,点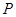 在直线
在直线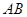 上且满足
上且满足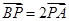 .(I)求点
.(I)求点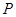 的轨迹的方程;(II)记点
的轨迹的方程;(II)记点 轨迹为曲线
轨迹为曲线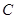 ,过点
,过点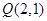 任作直线
任作直线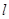 交曲线
交曲线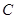 于
于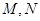 两点,过
两点,过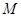 作斜率为
作斜率为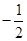 的直线
的直线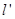 交曲线
交曲线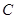 于另一点
于另一点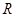 .求证:直线
.求证:直线 与直线
与直线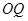 的交点为定点(
的交点为定点(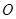 为坐标原点),并求出该定点.
为坐标原点),并求出该定点.
推荐套卷
(长为3的线段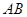 的两个端点
的两个端点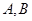 分别在
分别在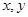 轴上移动,点
轴上移动,点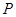 在直线
在直线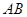 上且满足
上且满足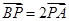 .(I)求点
.(I)求点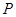 的轨迹的方程;(II)记点
的轨迹的方程;(II)记点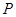 轨迹为曲线
轨迹为曲线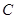 ,过点
,过点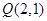 任作直线
任作直线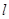 交曲线
交曲线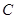 于
于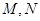 两点,过
两点,过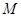 作斜率为
作斜率为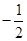 的直线
的直线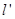 交曲线
交曲线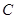 于另一点
于另一点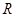 .求证:直线
.求证:直线 与直线
与直线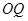 的交点为定点(
的交点为定点(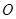 为坐标原点),并求出该定点.
为坐标原点),并求出该定点.