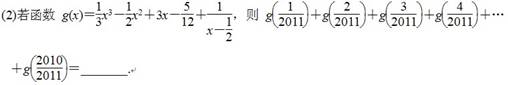对于三次函数f(x)＝ax3＋bx2＋cx＋d(a≠0)，定义：设f″(x)是函数y＝f(x)的导数
y＝f′(x)的导数，若方程f″(x)＝0有实数解x0，则称点(x0，f(x0))为函数y＝f(x)的“拐 点”．有同学发现“任何一个三次函数都有‘拐点’；任何一个三次函数都有对称中心；且‘拐点’就是对称中心．”请你将这一发现为条件，求
(1)函数f(x)＝x3－3x2＋3x对称中心为_______．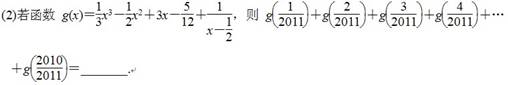
相关试题
中任选两个不同元素作为点的坐标，共有________个不同的点.
是第二象限的角，且
，则
的值是；推荐套卷
对于三次函数f(x)＝ax3＋bx2＋cx＋d(a≠0)，定义：设f″(x)是函数y＝f(x)的导数
y＝f′(x)的导数，若方程f″(x)＝0有实数解x0，则称点(x0，f(x0))为函数y＝f(x)的“拐 点”．有同学发现“任何一个三次函数都有‘拐点’；任何一个三次函数都有对称中心；且‘拐点’就是对称中心．”请你将这一发现为条件，求
(1)函数f(x)＝x3－3x2＋3x对称中心为_______．
粤公网安备 44130202000953号