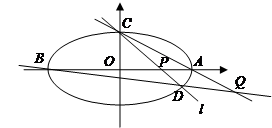.(本题14分)过点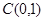 的椭圆
的椭圆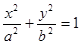 (
(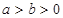 )的离心率为
)的离心率为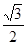 ,椭圆与
,椭圆与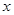 轴的交于两点
轴的交于两点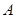 (
( ,
,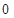 ),
),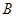 (
(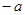 ,
,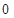 ),过点
),过点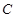 的直线
的直线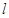 与椭圆交于另一点
与椭圆交于另一点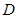 ,并与
,并与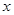 轴交于点
轴交于点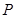 ,直线
,直线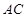 与直线
与直线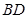 叫与点
叫与点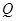 .
.
(I)当直线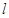 过椭圆右交点时,求线段
过椭圆右交点时,求线段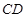 的长;
的长;
(II)当点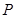 异于
异于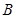 两点时,求证:
两点时,求证: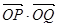 为定值.
为定值.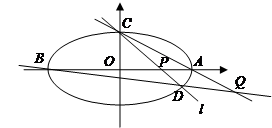
推荐套卷
.(本题14分)过点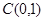 的椭圆
的椭圆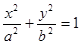 (
(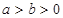 )的离心率为
)的离心率为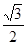 ,椭圆与
,椭圆与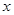 轴的交于两点
轴的交于两点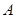 (
( ,
,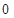 ),
),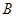 (
(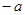 ,
,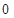 ),过点
),过点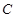 的直线
的直线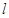 与椭圆交于另一点
与椭圆交于另一点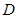 ,并与
,并与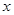 轴交于点
轴交于点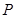 ,直线
,直线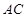 与直线
与直线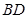 叫与点
叫与点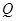 .
.
(I)当直线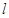 过椭圆右交点时,求线段
过椭圆右交点时,求线段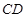 的长;
的长;
(II)当点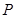 异于
异于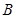 两点时,求证:
两点时,求证: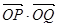 为定值.
为定值.