（本小题满分13分）已知m为实常数，设命题p：函数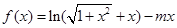
在其定义域内为减函数；命题
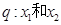是方程
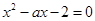的两上实根，不等式
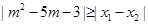对任意实数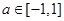
恒成立。
（1）当p是真命题，求m的取值范围；
（2）当“p或q”为真命题，“p且q”为假命题时，求m的取值范围。
相关试题
上恰有两个零点
，求tan（
）的值
，其中
为
．
满足
，求
的三个内角
所对的边分别为a，b，c，向量
，
，且
．
的大小；
，判断△
的不等式
，
，求a的值；
轴的正半轴为极轴建立极坐标系，已知曲线
的极坐标方程为
，过点
的直线
的参数方程为
（
为参数），直线
两点．
，求
的值．推荐套卷
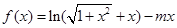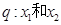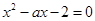（本小题满分13分）已知m为实常数，设命题p：函数在其定义域内为减函数；命题是方程的两上实根，不等式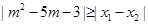对任意实数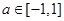恒成立。
（1）当p是真命题，求m的取值范围；
（2）当“p或q”为真命题，“p且q”为假命题时，求m的取值范围。
粤公网安备 44130202000953号