(本题满分18分)本题共有3个小题，第1小题满分6分，第2小题满分6分，第3小题满分6分．
已知函数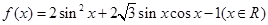
．
(1) 试说明函数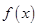
的图像是由函数
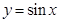的图像经过怎样的变换得到的；
(2) (理科)若函数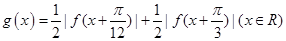
，试判断函数
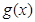的奇偶性，并用反证法证明函数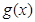的最小正周期是
；
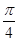(3) 求函数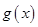
的单调区间和值域．
相关试题
满足
且
．
上, 
的图象上方，试确定实数
的范围．
－
（a>0，x>0）．
，2]上的值域是[
，
，
，求
；
，求实数a的取值范围．
，
，
， 
，
，求集合
(
∈R).
的图象；相关知识点
推荐套卷
(本题满分18分)本题共有3个小题，第1小题满分6分，第2小题满分6分，第3小题满分6分．
已知函数．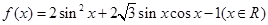
(1) 试说明函数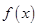的图像是由函数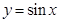的图像经过怎样的变换得到的；
(2) (理科)若函数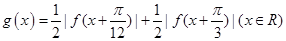，试判断函数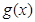的奇偶性，并用反证法证明函数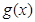的最小正周期是；
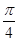(3) 求函数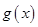的单调区间和值域．
粤公网安备 44130202000953号