在平面直角坐标系中，设点P到原点的距离为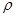
(希腊字母读作“柔”)，OP与X轴的正方向的夹角
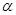，则用[
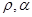]表示点P的极坐标。显然点P的坐标和它的极坐标存在一一对应关系。如点P的坐标(1,1)的极坐标为P[
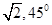],则极坐标Q[
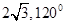]的坐标为
____________
的解是_____________相关知识点
推荐套卷
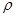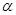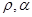在平面直角坐标系中，设点P到原点的距离为(希腊字母读作“柔”)，OP与X轴的正方向的夹角，则用[]表示点P的极坐标。显然点P的坐标和它的极坐标存在一一对应关系。如点P的坐标(1,1)的极坐标为P[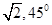],则极坐标Q[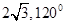]的坐标为
粤公网安备 44130202000953号