如图，矩形
的两条对角线相交于点
，
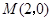边所在直线的方程为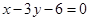
, 点
在
边所在直线上．
（1）求边所在直线的方程；
（2）求矩形外接圆的方程；
（3）若动圆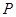
过点
，且与矩形
的外接圆外切，求动圆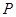的圆心的方程．
相关试题
(a，b为常数，且a≠0)，满足f(2)＝1，方程f(x)＝x有唯一实数解，求函数f(x)的解析式和f[f(－4)]的值．
，
，若
且
，求
的值
.
＋f(x)＝0.
, x∈[3, 5]
｝，B={x|
}，求
，
。推荐套卷
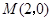如图，矩形的两条对角线相交于点，边所在直线的方程为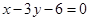, 点在边所在直线上．
（1）求边所在直线的方程；
（2）求矩形外接圆的方程；
（3）若动圆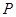过点，且与矩形
的外接圆外切，求动圆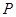的圆心的方程．
粤公网安备 44130202000953号