某集团对应聘者甲、乙、丙进行面试,并从专业知识、工作经验、仪表形象三方面给应聘者打分,每一方面满分10分,最后打分制成条形统计图如下.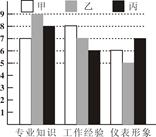
(1)利用图中提供的信息,在专业知识方面3人得分的平均分是多少?
(2)如果将专业知识、工作经验、仪表形象按6:3:1的比例计入总成绩,成绩高者应聘,那么应该录用哪一位应聘者?
相关知识点
推荐套卷
某集团对应聘者甲、乙、丙进行面试,并从专业知识、工作经验、仪表形象三方面给应聘者打分,每一方面满分10分,最后打分制成条形统计图如下.
(1)利用图中提供的信息,在专业知识方面3人得分的平均分是多少?
(2)如果将专业知识、工作经验、仪表形象按6:3:1的比例计入总成绩,成绩高者应聘,那么应该录用哪一位应聘者?