阅读下列材料:
题目:已知实数a,x满足a>2且x>2,试判断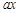 与
与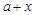 的大小关系,并加以说明.
的大小关系,并加以说明.
思路:可用“求差法”比较两个数的大小,先列出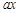 与
与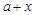 的差
的差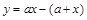 ,再
,再
说明y的符号即可.
现给出如下利用函数解决问题的方法:
简解:可将y的代数式整理成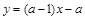 ,要判断y的符号可借助函数
,要判断y的符号可借助函数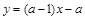 的图象和性质解决.
的图象和性质解决.
参考以上解题思路解决以下问题:
已知a,b,c都是非负数,a<5,且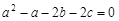 ,
, .
.(1)分别用含a的代数式表示4b,4c;
(2)说明a,b,c之间的大小关系.
相关知识点
推荐套卷




 (k是常数).
(k是常数). 和
和 的图像如图所示,请你在同一坐标系中画出k=3时函数
的图像如图所示,请你在同一坐标系中画出k=3时函数 的图像;
的图像;
 的图像向左平移2个单位,再向下平移4个单位,得到函数
的图像向左平移2个单位,再向下平移4个单位,得到函数 的图像。请写出函数
的图像。请写出函数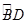 的中点,CE⊥AB于点E,BD交CE于点F.
的中点,CE⊥AB于点E,BD交CE于点F.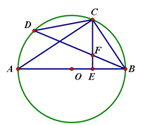
 粤公网安备 44130202000953号
粤公网安备 44130202000953号