已知两条不同直线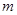 、
、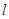 ,两个不同平面
,两个不同平面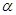 、
、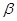 ,给出下列命题:
,给出下列命题:
①若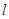 垂直于
垂直于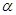 内的两条相交直线,则
内的两条相交直线,则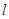 ⊥
⊥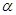 ;
;
②若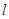 ∥
∥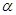 ,则
,则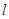 平行于
平行于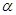 内的所有直线;
内的所有直线;
③若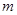

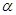 ,
,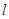

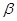 且
且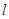 ⊥
⊥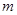 ,则
,则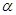 ⊥
⊥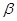 ;
;
④若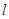

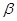 ,
, ,则
,则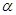 ⊥
⊥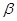 ;
;
⑤若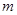

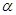 ,
,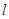

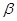 且
且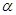 ∥
∥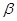 ,则
,则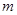 ∥
∥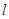 ;
;
其中正确命题的序号是 .(把你认为正确命题的序号都填上)
推荐套卷
已知两条不同直线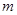 、
、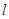 ,两个不同平面
,两个不同平面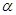 、
、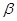 ,给出下列命题:
,给出下列命题:
①若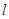 垂直于
垂直于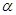 内的两条相交直线,则
内的两条相交直线,则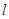 ⊥
⊥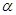 ;
;
②若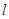 ∥
∥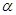 ,则
,则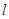 平行于
平行于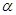 内的所有直线;
内的所有直线;
③若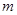

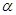 ,
,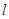

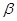 且
且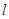 ⊥
⊥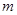 ,则
,则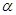 ⊥
⊥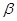 ;
;
④若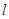

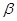 ,
, ,则
,则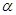 ⊥
⊥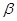 ;
;
⑤若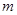

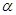 ,
,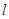

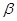 且
且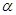 ∥
∥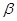 ,则
,则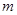 ∥
∥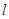 ;
;
其中正确命题的序号是 .(把你认为正确命题的序号都填上)