（2011河北，18，3分）如图9，给正五边形的顶点依次编号为1，2，3，4，5.若从某一顶点开始，沿正五边形的边顺时针方向行走，顶点编号的数字是几，就走几个边长，则称这种走法为一次“移位”.如：小宇在编号为3的顶点上时，那么他应走3个边长，即从3→4→5→1为第一次“移位”，这时他到达编号为1的顶点；然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始，第10次“移位”后，则他所处顶点的编号为_ _．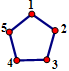
的相反数等于_________.
解集是 ．相关知识点
推荐套卷
（2011河北，18，3分）如图9，给正五边形的顶点依次编号为1，2，3，4，5.若从某一顶点开始，沿正五边形的边顺时针方向行走，顶点编号的数字是几，就走几个边长，则称这种走法为一次“移位”.如：小宇在编号为3的顶点上时，那么他应走3个边长，即从3→4→5→1为第一次“移位”，这时他到达编号为1的顶点；然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始，第10次“移位”后，则他所处顶点的编号为_ _．
粤公网安备 44130202000953号