（本小题满分10分）如图，在四棱锥S—ABCD中，侧棱SA＝SB＝SC＝SD，底面ABCD是菱形，AC与BD交于O点．
(Ⅰ)求证：AC⊥平面SBD；
(Ⅱ)若E为BC中点，点P在侧面△SCD内及其边界上运动，并保持PE⊥AC，试指出动点P的轨迹，并证明你的结论．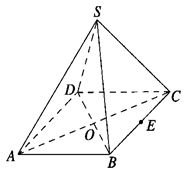
中，已知BC边上的高所在直线的方程为
,
平分线所在直线的方程为
，若点B的坐标为（1，2），
中，点
是
的中点.
平面
；
平面
.
，弧长为
，求此扇形内切圆的面积。
，两角和为1 
，求这两角的弧度数。
，
角的7倍角的终边和推荐套卷
（本小题满分10分）如图，在四棱锥S—ABCD中，侧棱SA＝SB＝SC＝SD，底面ABCD是菱形，AC与BD交于O点．
(Ⅰ)求证：AC⊥平面SBD；
(Ⅱ)若E为BC中点，点P在侧面△SCD内及其边界上运动，并保持PE⊥AC，试指出动点P的轨迹，并证明你的结论．
粤公网安备 44130202000953号