如图，三棱柱ABC-A1B1C1的底面是边长为3的正三角形，侧棱AA1垂直于底面ABC，AA1=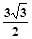
，D是CB延长线上一点，且BD=BC.
（1）求证：直线BC1∥平面AB1D；
（2）求二面角B1-AD-B的大小；
（3）求三棱锥C1-ABB1的体积。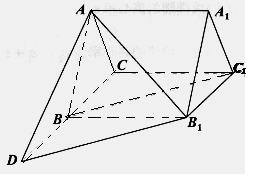
相关试题
，
，△
的周长为6．
的轨迹
的方程；
与曲线
，
．若点
在
轴上，且
，求点
中，底面
是正方形．已知
，
.
；
．
的圆心
，被
轴截得的弦长为
．
交于
，
两点，且
，求
的值．
中，
， 
，若
是
中点．
∥平面
；
所成的角.
的右焦点
重合，过点
的直线与抛物线交于
，
两点.
的面积．推荐套卷
如图，三棱柱ABC-A1B1C1的底面是边长为3的正三角形，侧棱AA1垂直于底面ABC，AA1=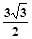，D是CB延长线上一点，且BD=BC.
（1）求证：直线BC1∥平面AB1D；
（2）求二面角B1-AD-B的大小；
（3）求三棱锥C1-ABB1的体积。
粤公网安备 44130202000953号