(本小题满分12分)
设数列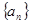 的前
的前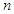 项和为
项和为 ,点
,点 在直线
在直线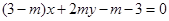 上,(
上,( 为常数,
为常数,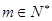 ,
,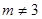 ).
).
(1)求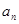 ;
;
(2)若数列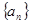 的公比
的公比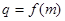 ,数列
,数列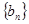 满足
满足 ,
,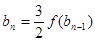 ,
, ,求证:
,求证: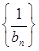 为等差
为等差 数列,并求
数列,并求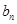 ;
;
(3)设数列 满足
满足 ,
,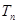 为数列
为数列 的前
的前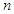 项和,且存在实数
项和,且存在实数 满足
满足
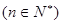 ,求
,求 的最大值.
的最大值.
推荐套卷
(本小题满分12分)
设数列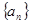 的前
的前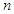 项和为
项和为 ,点
,点 在直线
在直线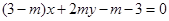 上,(
上,( 为常数,
为常数,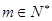 ,
,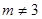 ).
).
(1)求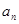 ;
;
(2)若数列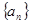 的公比
的公比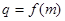 ,数列
,数列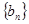 满足
满足 ,
,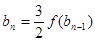 ,
, ,求证:
,求证: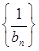 为等差
为等差 数列,并求
数列,并求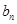 ;
;
(3)设数列 满足
满足 ,
,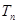 为数列
为数列 的前
的前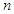 项和,且存在实数
项和,且存在实数 满足
满足
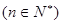 ,求
,求 的最大值.
的最大值.