为了测量两山顶M,N间的距离,飞机沿水平方向在A,B两点进行测量,A,B,M,N在同一个铅垂平面内(如示意图),飞机能够测量的数据有俯角和A,B间的距离,请设计一个方案,包括:①指出需要测量的数据(用字母表示,并在图中标出);②用文字和公式写出计算M,N间的距离的步骤。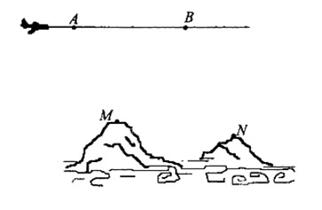
相关知识点
推荐套卷
为了测量两山顶M,N间的距离,飞机沿水平方向在A,B两点进行测量,A,B,M,N在同一个铅垂平面内(如示意图),飞机能够测量的数据有俯角和A,B间的距离,请设计一个方案,包括:①指出需要测量的数据(用字母表示,并在图中标出);②用文字和公式写出计算M,N间的距离的步骤。