如图，已知抛物线
交x轴的正半轴于点A，交y轴于点B．求A、B两点的坐标，并求直线AB的解析式；
设
（
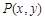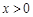）是直线
上的一点，Q是OP的中点（O是原点），以PQ为对角线作正方形PEQF．若正方形PEQF与直线AB有公共点，求x的取值范围；在（2）的条件下，记正方形PEQF与△OAB公共部分的面积为S，求S关于x的函数解析式，并探究S的最大值．
，
），且抛物线经过点（
，
），求抛物线的表达式．
．
+(x－2)(x+2)－4x(x－
)相关知识点
推荐套卷
如图，已知抛物线交x轴的正半轴于点A，交y轴于点B．求A、B两点的坐标，并求直线AB的解析式；
设
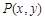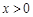（）是直线上的一点，Q是OP的中点（O是原点），以PQ为对角线作正方形PEQF．若正方形PEQF与直线AB有公共点，求x的取值范围；在（2）的条件下，记正方形PEQF与△OAB公共部分的面积为S，求S关于x的函数解析式，并探究S的最大值．
粤公网安备 44130202000953号