(本小题满分14分)若 ,
,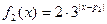 ,
,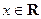 ,
,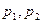 为常
为常
数,且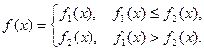
(Ⅰ)求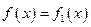 对所有实数成立的充要条件(用
对所有实数成立的充要条件(用 表示);
表示);
(Ⅱ)设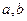 为两实数,
为两实数,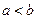 且
且
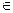
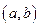 ,若
,若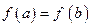
求证: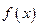 在区间
在区间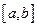 上的单调增区间的长度和为
上的单调增区间的长度和为 (闭区间
(闭区间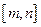 的长度定义为
的长度定义为 ).
).
相关知识点
推荐套卷
(本小题满分14分)若 ,
,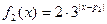 ,
,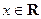 ,
,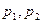 为常
为常
数,且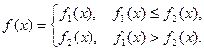
(Ⅰ)求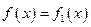 对所有实数成立的充要条件(用
对所有实数成立的充要条件(用 表示);
表示);
(Ⅱ)设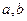 为两实数,
为两实数,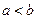 且
且
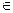
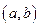 ,若
,若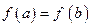
求证: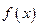 在区间
在区间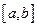 上的单调增区间的长度和为
上的单调增区间的长度和为 (闭区间
(闭区间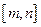 的长度定义为
的长度定义为 ).
).