下列说法
①如图,扇形 的圆心角
的圆心角 ,点
,点 是
是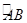 上异于
上异于 的动点,过点
的动点,过点 作
作 于
于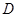 ,作
,作 于
于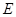 ,连接
,连接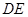 ,点
,点 在线段
在线段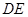 上,且
上,且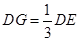 ,连接
,连接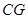 。当点
。当点 在
在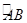 上运动时,在
上运动时,在 中,长度不变的是
中,长度不变的是 ;
;

②如图,正方形纸片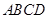 的边长为
的边长为 ,⊙
,⊙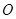 的半径为
的半径为 ,圆心
,圆心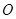 在正方形的中心上,将纸片按图示方式折叠,折叠后点
在正方形的中心上,将纸片按图示方式折叠,折叠后点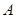 于点
于点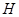 重合,且
重合,且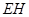 切⊙
切⊙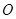 于点
于点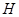 ,延长
,延长 交
交 边于点
边于点 ,则
,则 的长为
的长为 ;
;
③已知 中,
中, ,则其内心和外心之间的距离是
,则其内心和外心之间的距离是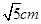 。其中正确的有 (请写序号,少选,错选均不得分)
。其中正确的有 (请写序号,少选,错选均不得分)
相关知识点
推荐套卷
 ,第2次从点
,第2次从点 ,第3次从点
,第3次从点 向左移动9个单位长度至点
向左移动9个单位长度至点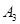 ,…,按照这种移动方式进行下去,点
,…,按照这种移动方式进行下去,点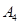 表示的数是,如果点
表示的数是,如果点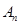 与原点的距离不小于20,那么
与原点的距离不小于20,那么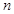 的最小值是.
的最小值是.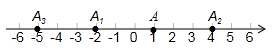


 =.
=. 粤公网安备 44130202000953号
粤公网安备 44130202000953号