(本题满分12分)
已知点C为线段AB上一点, 分别以AC、BC为边在线段AB同侧作△ACD和△BCE, 且CA=CD, CB=CE, ∠ACD=∠BCE, 直线AE与BD交于点F.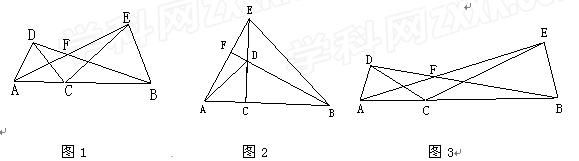
(1)如图1,求证:△ACE≌△DCB。
(2)如图1, 若∠ACD=60°, 则∠AFB= ;
如图2, 若∠ACD=90°, 则∠AFB= ;
(3)如图3, 若∠ACD=β, 则∠AFB= (用含β的式子表示)
并说明理由。
相关知识点
推荐套卷

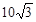 海里处的B港出发向东航行,观察站第一次测得该船在A地北偏东30°的C处;半小时后,又测得该船在A地的北偏东60°的D处,求此船的速度.
海里处的B港出发向东航行,观察站第一次测得该船在A地北偏东30°的C处;半小时后,又测得该船在A地的北偏东60°的D处,求此船的速度.
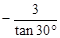 ;
; 粤公网安备 44130202000953号
粤公网安备 44130202000953号