一次棋赛,有n个女选手和9n个男选手,每位参赛者与其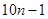 个选手各对局一次,计分方式为:胜者的2分,负者得0分,平局各自得1分。比赛结束后统计发现所有参赛男选手的分数和是所有女选手的分数和的4倍,则n的所有可能值是 .
个选手各对局一次,计分方式为:胜者的2分,负者得0分,平局各自得1分。比赛结束后统计发现所有参赛男选手的分数和是所有女选手的分数和的4倍,则n的所有可能值是 .
相关知识点
推荐套卷
一次棋赛,有n个女选手和9n个男选手,每位参赛者与其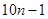 个选手各对局一次,计分方式为:胜者的2分,负者得0分,平局各自得1分。比赛结束后统计发现所有参赛男选手的分数和是所有女选手的分数和的4倍,则n的所有可能值是 .
个选手各对局一次,计分方式为:胜者的2分,负者得0分,平局各自得1分。比赛结束后统计发现所有参赛男选手的分数和是所有女选手的分数和的4倍,则n的所有可能值是 .