给出下列命题:
(1)存在实数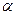 ,使
,使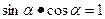 ;
;
(2)函数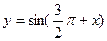 是偶函数;
是偶函数;
(3)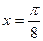 是函数
是函数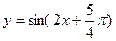 的一条对称轴;
的一条对称轴;
(4)若 是第一象限的角,且
是第一象限的角,且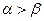 ,则
,则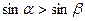 ;
;
(5)将函数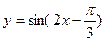 的图像先向左平移
的图像先向左平移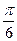 ,然后将所得图像上所有点的横坐标变为原来的2倍(纵坐标不变),所得到的图像对应的解析式为
,然后将所得图像上所有点的横坐标变为原来的2倍(纵坐标不变),所得到的图像对应的解析式为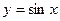 .
.
其中真命题的序号是
推荐套卷
给出下列命题:
(1)存在实数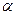 ,使
,使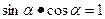 ;
;
(2)函数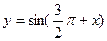 是偶函数;
是偶函数;
(3)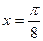 是函数
是函数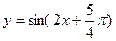 的一条对称轴;
的一条对称轴;
(4)若 是第一象限的角,且
是第一象限的角,且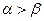 ,则
,则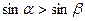 ;
;
(5)将函数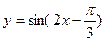 的图像先向左平移
的图像先向左平移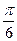 ,然后将所得图像上所有点的横坐标变为原来的2倍(纵坐标不变),所得到的图像对应的解析式为
,然后将所得图像上所有点的横坐标变为原来的2倍(纵坐标不变),所得到的图像对应的解析式为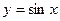 .
.
其中真命题的序号是