(满分l4分)如图，已知AB为⊙O的直径，弦CD⊥AB，垂足为点H．
(1)求证：AH·AB=AC2；
(2)若过点A的直线与弦CD(不含端点)相交于点E，与⊙O相交于点F，求证：AE·AF=AC2；
(3)若过点A的直线与直线CD相交于点P，与⊙O相交于点Q，判断AP·AQ=AC2是否成立(不必证明)．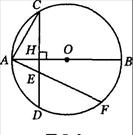
和方程组
有相同的解，则m的值是.
的解是
，则a+b的值为.推荐套卷
(满分l4分)如图，已知AB为⊙O的直径，弦CD⊥AB，垂足为点H．
(1)求证：AH·AB=AC2；
(2)若过点A的直线与弦CD(不含端点)相交于点E，与⊙O相交于点F，求证：AE·AF=AC2；
(3)若过点A的直线与直线CD相交于点P，与⊙O相交于点Q，判断AP·AQ=AC2是否成立(不必证明)．
粤公网安备 44130202000953号