(满分l3分)如图,对称轴为直线x=一 的抛物线经过点A(-6,0)和点B(0,4).
的抛物线经过点A(-6,0)和点B(0,4).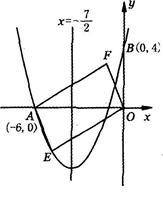
(1)求抛物线的解析式和顶点坐标;
(2)设点E(x,y)是抛物线上的一个动点,且位于第三象限,四边形OEAF是以OA为对角线的平行四边形,求□OEAF的面积S与x的函数关系式,并写出自变量x的取值范围;
①当□OEAF的面积为24时,请判断□OEAF是否为菱形?
②是否存在点E,使□OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.
相关知识点
推荐套卷
 粤公网安备 44130202000953号
粤公网安备 44130202000953号