(满分l2分)某中学学生会为了解该校学生喜欢球类活动的情况,采取抽样调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了若干名学生的兴趣爱好,并将调查的结果绘制成如下的两幅不完整的统计图(如图,要求每位同学只能选择一种自己喜欢的球类;图中用乒乓球、足球、排球、篮球代表喜欢这四种球类中的某一种球类的学生人数),请你根据图中提供的信息解答下列问题:
(1)在这次研究中,一共调查了多少位学生?
(2)喜欢排球的人数在扇形统计图中所占的圆心角是多少度?
(3)请补全频数分布折线统计图.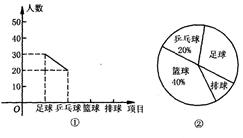
相关知识点
推荐套卷

 车的拥有量达到100辆,求2007年底到2009年底家庭轿车的拥有量的年平均增长率?(12’)
车的拥有量达到100辆,求2007年底到2009年底家庭轿车的拥有量的年平均增长率?(12’)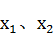 是一元二次方程
是一元二次方程 的两个实数根,求实数m的取值范围. (10’)
的两个实数根,求实数m的取值范围. (10’) ,用含有a、b的代数式表示
,用含有a、b的代数式表示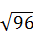 . (10’)
. (10’) 两根互为相反数?
两根互为相反数? (10’)
(10’) 粤公网安备 44130202000953号
粤公网安备 44130202000953号