为了让更多的人参与2011年在深圳举办的“大运会”,深圳某旅游公司向国内外发行总量为2000万张的旅游优惠卡,其中向境外人士发行的是旅游金卡(简称金卡),向境内人士发行的是旅游银卡(简称银卡)。现有一个由36名游客组成的旅游团到深圳参观旅游,其中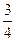 是境外游客,其余是境内游客。在境外游客中有
是境外游客,其余是境内游客。在境外游客中有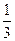 持金卡,在境内游客中有
持金卡,在境内游客中有 持银卡
持银卡
(Ⅰ)在该团中随机采访3名游客,求恰有1人持金卡且持银卡者少于2人的概率
(Ⅱ)在该 团的省内游客中随机采访3名
团的省内游客中随机采访3名 游客,设其中持银卡人数为随机变量
游客,设其中持银卡人数为随机变量 ,求
,求 的分布列及数学期望
的分布列及数学期望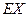
推荐套卷
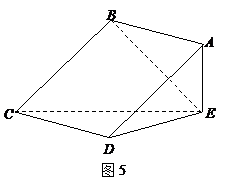
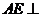 平面CDE,且
平面CDE,且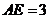 ,
,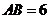 .
. 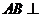 平面
平面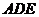 ;
;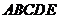 的体积.
的体积.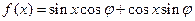 (其中
(其中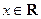 ,
,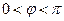 ).
).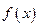 的最小正周期;
的最小正周期;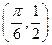 在函数
在函数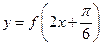 的图像上,求
的图像上,求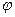 的值.
的值.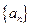 满足对任意的
满足对任意的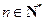 ,都有
,都有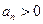 ,
,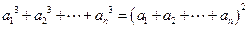 .
.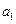 ,
,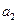 的值;
的值;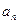 ;
; 的前
的前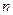 项和为
项和为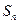 ,不等式
,不等式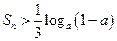 对任意的正整数
对任意的正整数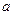 的取值范围.
的取值范围.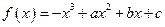 在
在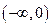 上是减函数,在
上是减函数,在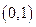 上是增函数,函数
上是增函数,函数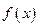 在
在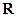 上有三个零点,且1是其中一个零点.
上有三个零点,且1是其中一个零点.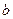 的值;
的值;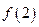 的取值范围;
的取值范围;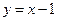 与函数
与函数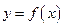 的图像交点个数的情况,并说明理由.
的图像交点个数的情况,并说明理由.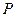 到定点
到定点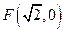 的距离与点
的距离与点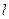 :
: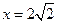 的距离之比为
的距离之比为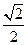 .
.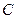 的方程;
的方程;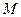 、
、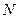 是直线
是直线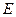 与点
与点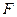 关于原点
关于原点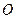 对称,若
对称,若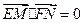 ,求
,求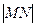 的最小值.
的最小值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号