(本题10分)
(1)拼一拼,画一画:请你用4个长为a,宽为b的矩形拼成一个大正方形,并且正中间留下一个洞,这个洞恰好是一个小正方形。
(2)用不同方法计算中间的小正方形的面积,聪明的你能发现什么?
(3)当拼成的这个大正方形边长比中间小正方形边长多3cm时,它的面积就多24cm2,求中间小正方形的边长。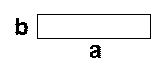
(本题10分)
(1)拼一拼,画一画:请你用4个长为a,宽为b的矩形拼成一个大正方形,并且正中间留下一个洞,这个洞恰好是一个小正方形。
(2)用不同方法计算中间的小正方形的面积,聪明的你能发现什么?
(3)当拼成的这个大正方形边长比中间小正方形边长多3cm时,它的面积就多24cm2,求中间小正方形的边长。