已知某种水果的批发单价与批发量的函数关系如图（1）所示．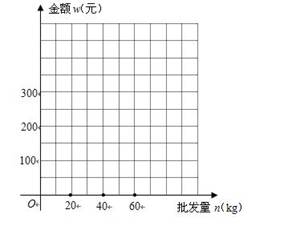
(1). 请说明图中①、②两段函数图象的实际意义；
(2). 写出批发该种水果的资金金额w（元）与批发量n（kg）之间的函数关系式；在下图的坐标系中画出该函数图象；指出金额在什么范围内，以同样的资金可以批发到较多数量的该种水果.
(3). 经调查，某经销商销售该种水果的日最高销量与零售价之间的函数关系如图（2）所示，该经销商拟每日售出60kg以上该种水果，且当日零售价不变，请你帮助该经销商设计进货和销售的方案，使得当日获得的利润最大．
相关试题
，BD=2，求BC的长。
)
＋(-1) 
如图，在
中，
，
，把边长分别为
的
个正方形依次放入
中，请回答下列问题：
（1）按要求填表
|
1 |
2 |
3 |
 |
（2）第个正方形的边长
；
（3）若
是正整数，且
，试判断的关系．
如图，把菱形ABCD沿着BD的方向平移到菱形A/B/C/D/′的位置，
(1)求证：重叠部分的四边形B/EDF/是菱形
(2)若重叠部分的四边形B/EDF/
面积是把菱形ABCD面积的一半,且BD=
，求则此菱形移动的距离．
3，CB="5" ，求DE的长.
粤公网安备 44130202000953号