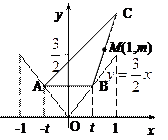（本小题12分）如图，函数y=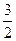
|x|在x∈[－1,1]的图象上有两点A、B，
AB∥
Ox轴，点M（1，m）（m是已知实数，且m>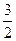）是△ABC的边BC的中点。
（Ⅰ）写出用B的横坐标t表示△ABC面积S的函数解析式S＝f(t)；
（Ⅱ）求函数S＝f(t)的最大值，并求出相应的C点坐标。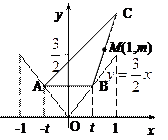
相关试题
＋(m2＋2m－3)i，当m为何值时．
＋(m2－5m－6)i(m∈R)，试求实数m分别取什么值时，z分别为：
sinx，sinx)，b＝(cosx，sinx)，x∈
.推荐套卷
（本小题12分）如图，函数y=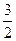|x|在x∈[－1,1]的图象上有两点A、B，AB∥
Ox轴，点M（1，m）（m是已知实数，且m>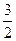）是△ABC的边BC的中点。
（Ⅰ）写出用B的横坐标t表示△ABC面积S的函数解析式S＝f(t)；
（Ⅱ）求函数S＝f(t)的最大值，并求出相应的C点坐标。
粤公网安备 44130202000953号