图10是小红设计的钻石形商标，△ABC是边长为2的等边三角形，四边形ACDE是等腰梯形，AC∥ED，∠EAC=60°，AE=1．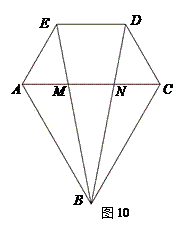
（1）证明：△ABE≌△CBD；
（2）图中存在多对相似三角形，请你找出一对进
行证明，并求出其相似比（不添加辅助线，
不找全等的相似三角形）；
（3）小红发现AM=MN=NC，请证明此结论；
（4）求线段BD的长．
相关试题
图10是小红设计的钻石形商标，△ABC是边长为2的等边三角形，四边形ACDE是等腰梯形，AC∥ED，∠EAC=60°，AE=1．
（1）证明：△ABE≌△CBD；
（2）图中存在多对相似三角形，请你找出一对进
行证明，并求出其相似比（不添加辅助线，
不找全等的相似三角形）；
（3）小红发现AM=MN=NC，请证明此结论；
（4）求线段BD的长．
， 6 ，
，0，
，写出整数的和与分数的积的差
，
，
，
这六个数中，负数有m个，整数有n个，非负数有k个，求
的值。
，
， 0， -|-2︳， 2．5 |-3︳
中，直线AB交
轴于A（2，0），交
轴负半轴于B（0，-10），C为x轴正半轴上一点，且OC=5OA．
的大小是否发生变化？若改变，请说明理由；若不变，求出这个比值．
粤公网安备 44130202000953号