（本小题满分7分）已知：等边三角形ABC
（1）如图1，P为等边△ABC外一点，且∠
BPC=120°．试猜想线段BP、PC、AP之间的数量关系,并证明
你的猜想；
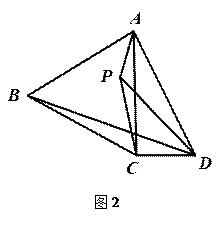
（2）如图2，P为等边△ABC内一点，且∠APD=120°．求证：PA+PD+PC＞BD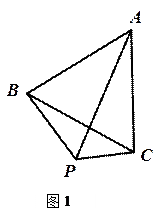
（本小题满分7分）已知：等边三角形ABC
（1）如图1，P为等边△ABC外一点，且∠BPC=120°．试猜想线段BP、PC、AP之间的数量关系,并证明你的猜想；
（2）如图2，P为等边△ABC内一点，且∠APD=120°．求证：PA+PD+PC＞BD
粤公网安备 44130202000953号