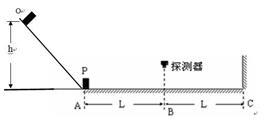
如图所示,倾角为450的光滑轨道OA和水平轨道AC在A处用一小段光滑圆弧轨道平滑连接,AC段的中点B的正上方有一探测器,探测器只能探测处于其正下方的物体,C处有一竖直挡板,AC间的动摩擦因素为μ=0.1.一小物块P自倾斜轨道OA上离水平轨道AC高h处由静止释放,以小物块P运动到A处的时刻为计时零点,探测器只在t1=2s至t2=6s内工作,已知P的质量为m=1kg, AB段长为L=4m,g取10m/s2,P视为质点,P与挡板碰撞后原速率反弹.(结果不用取近似值)
(1)若h=1.2m,求P与挡板碰撞反弹后运动到B点所用的时间。
(2)若P与挡板碰撞后,能在探测器的工作时间内通过B点,求h的取值范围。