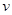如图所示,在竖直方向上A、B两物体通过劲度系数为k的轻质弹簧相连,A放在水平地面上;B、C两物体通过细绳绕过轻质定滑轮相连,C放在固定的光滑斜面上.用手拿住C,使细线刚刚拉直但无拉力作用,并保证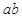 段的细线竖直、cd段的细线与斜面平行.已知A、B的质量均为
段的细线竖直、cd段的细线与斜面平行.已知A、B的质量均为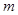 ,C的质量为4
,C的质量为4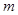 ,重力加速度为g,细线与滑轮之间的摩擦不计,开始时整个系统处于静止状态.释放C后它沿斜面下滑(斜面足够长), A刚离开地面时, B获得最大速度,求:
,重力加速度为g,细线与滑轮之间的摩擦不计,开始时整个系统处于静止状态.释放C后它沿斜面下滑(斜面足够长), A刚离开地面时, B获得最大速度,求: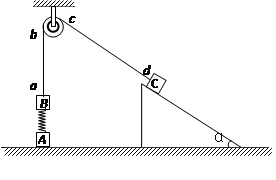
(1)斜面倾角α.
(2)B的最大速度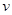
如图所示,在竖直方向上A、B两物体通过劲度系数为k的轻质弹簧相连,A放在水平地面上;B、C两物体通过细绳绕过轻质定滑轮相连,C放在固定的光滑斜面上.用手拿住C,使细线刚刚拉直但无拉力作用,并保证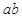 段的细线竖直、cd段的细线与斜面平行.已知A、B的质量均为
段的细线竖直、cd段的细线与斜面平行.已知A、B的质量均为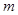 ,C的质量为4
,C的质量为4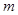 ,重力加速度为g,细线与滑轮之间的摩擦不计,开始时整个系统处于静止状态.释放C后它沿斜面下滑(斜面足够长), A刚离开地面时, B获得最大速度,求:
,重力加速度为g,细线与滑轮之间的摩擦不计,开始时整个系统处于静止状态.释放C后它沿斜面下滑(斜面足够长), A刚离开地面时, B获得最大速度,求:
(1)斜面倾角α.
(2)B的最大速度