(本小题满分7分)
有三张形状、大小、质地完全一致的卡片,在每张卡片上分别写上0,1,2,现从中任意抽取一张,将其上的数字记作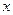 ,然后放回,再抽取一张,将其上的数字记作
,然后放回,再抽取一张,将其上的数字记作 ,令
,令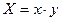 。
。
(Ⅰ)求 所取各值的概率;
所取各值的概率;
(Ⅱ)求 的分布列,并求出
的分布列,并求出 的数学期望值。
的数学期望值。
推荐套卷
(本小题满分7分)
有三张形状、大小、质地完全一致的卡片,在每张卡片上分别写上0,1,2,现从中任意抽取一张,将其上的数字记作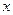 ,然后放回,再抽取一张,将其上的数字记作
,然后放回,再抽取一张,将其上的数字记作 ,令
,令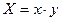 。
。
(Ⅰ)求 所取各值的概率;
所取各值的概率;
(Ⅱ)求 的分布列,并求出
的分布列,并求出 的数学期望值。
的数学期望值。