给出下列命题：
①.在等差数列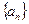
中
，且
，则使数列前n项和
取最小值的n等于5；
②
的外接圆的圆心为O，半径为1，
，且
，则向量
在向量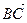
方向上的投影为
；
③曲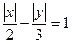线
与直线
有两个交点，则
的取值范围是
或
；
④若定义在区间D上的函数f(x)对于D上任意n个值x1、x2、…xn总满足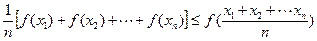
，则f(x)称为D上的凸函
数，现已知
在
上凸函数，则锐角△ABC中
的最大值为
。
其中正确命题的序号是 。
的焦点坐标是_______.
的定义域为R，且
一定是偶函数；
都有
，则
，则
对称；
，且
，若
恒成立，则
上的增函数。
满足约束条件
，则
的最大值是_______.
推荐套卷
给出下列命题：
①.在等差数列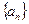中，且 ，则使数列前n项和 取最小值的n等于5；
②的外接圆的圆心为O，半径为1，，且，则向量在向量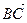方向上的投影为；
③曲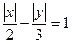线与直线有两个交点，则的取值范围是或；
④若定义在区间D上的函数f(x)对于D上任意n个值x1、x2、…xn总满足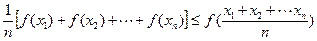 ，则f(x)称为D上的凸函数，现已知在上凸函数，则锐角△ABC中的最大值为。
其中正确命题的序号是 。
粤公网安备 44130202000953号