(本小题满分12分)如图,四边形 是边
是边 长为1的正方形,
长为1的正方形, 平面
平面 ,
,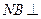 平面
平面 ,且
,且
(1)以向量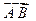 方向为侧视方向,侧视图是什么形状?说明理由并画出侧视图。
方向为侧视方向,侧视图是什么形状?说明理由并画出侧视图。
(2)求证: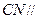 平面
平面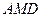 ;
;
(3)证明:平面ANC⊥平面BDMN
相关知识点
推荐套卷
(本小题满分12分)如图,四边形 是边
是边 长为1的正方形,
长为1的正方形, 平面
平面 ,
,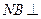 平面
平面 ,且
,且
(1)以向量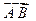 方向为侧视方向,侧视图是什么形状?说明理由并画出侧视图。
方向为侧视方向,侧视图是什么形状?说明理由并画出侧视图。
(2)求证: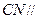 平面
平面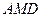 ;
;
(3)证明:平面ANC⊥平面BDMN