(11·大连)(本题12分)如图7,某建筑物BC上有一旗杆AB,小明在与BC
相距12m的F处,由E点观测到旗杆顶部A的仰角为52°、 底部B的仰角为45°,小明的
底部B的仰角为45°,小明的
观测点与地面的距离EF为1.6m.
⑴求建筑物BC的高度;
⑵求旗杆AB的高度.
(结果精确到 0.1m.参考数据
0.1m.参考数据 :
: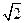 ≈1.41,sin52°≈0.79,tan52°≈1.28)
≈1.41,sin52°≈0.79,tan52°≈1.28)
相关知识点
推荐套卷
(11·大连)(本题12分)如图7,某建筑物BC上有一旗杆AB,小明在与BC
相距12m的F处,由E点观测到旗杆顶部A的仰角为52°、 底部B的仰角为45°,小明的
底部B的仰角为45°,小明的
观测点与地面的距离EF为1.6m.
⑴求建筑物BC的高度;
⑵求旗杆AB的高度.
(结果精确到 0.1m.参考数据
0.1m.参考数据 :
: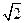 ≈1.41,sin52°≈0.79,tan52°≈1.28)
≈1.41,sin52°≈0.79,tan52°≈1.28)