(本题满分9分)如图9,已知线段AB的长为2a，点P是AB上的动点（P不与A，B重合），分别以AP、PB为边向线段AB的同一侧作正△APC和正△PBD．
（1）当△APC与△PBD的面积之生取最小值时，AP=
；（直接写结果）
（2）连结AD、BC，相交于点Q，设∠AQC=α，那么α的大小是否会随点P的移动面变化？请说明理由；
（3）如图10，若点P固定，将△PBD绕点P按顺时针方向旋转（旋转角小于
180°），此时α的大小是否发生变化？（只需直接写出你的猜想，不必证明）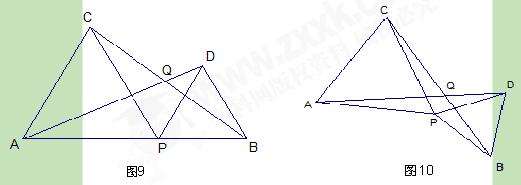
相关试题
如图，在⊙O中，直径AB垂直于弦CD，垂足为E，连接AC，将△ACE沿AC翻折得到△ACF，直线FC与直线AB相交于点G．问：
（1）直线FC与⊙O有何位置关系？说明理由；
（2）若OB＝BG＝2，求CD的长；
如图，已知A（－4，
）B（－1，2）是一次函数
与反比例函数
图象的两个交点，AC⊥x轴于C，BD⊥y轴于D; 
（1）根据图象直接回答：在第二象限内，当x取何值时，一次函数大于反比例函数的值？
（2）求一次函数解析式及m的值；
（3）P是线段AB上的一点，连接PC，PD，若△PCA和△PDB面积相等，求点P的坐标
米/分的速度平行海面飞行20分钟到达B处后，测得搜救船在俯角为60°的海面D处，求搜救船搜寻的平均速度．（结果保留一个有效数字，参考数据：
≈1．414，
≈1．732）．
相关知识点
推荐套卷
粤公网安备 44130202000953号