王老师对河东中学九（一）班的某次模拟考试成绩进行统计后，绘制了频数分布直方图（如图，分数取正整数，满分120分）．根据图形，回答下列问题：（直接填写结果）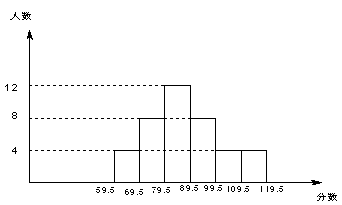
（1）该班有
名学生；
（2）89.5 --99.5这一组的频数是 ，频率是
（3）估算该班这次数学模拟考试的平均成绩 是．
有解，求k的取值范围。
，
，
，……
，试求
的值。
，B=
，求（3A-2B）－（2A+B）的值。
，其中
。相关知识点
推荐套卷
王老师对河东中学九（一）班的某次模拟考试成绩进行统计后，绘制了频数分布直方图（如图，分数取正整数，满分120分）．根据图形，回答下列问题：（直接填写结果）
（1）该班有名学生；
（2）89.5 --99.5这一组的频数是 ，频率是
（3）估算该班这次数学模拟考试的平均成绩 是．
粤公网安备 44130202000953号