某中学在一次法律知识测试中,抽取部分学生成绩(分数为整
数,满分100分)将所得得数据整理后,画出频率分布直方图,已
知图中从左到右的三个小组的频率分别为0.04,0.06,0.82,第二
小组的频数为3.
(1)本次测试中抽样的学生有多少人?
(2)分数在90.5~100.5这一组的频率是多少?有多少人?
(3)若这次成绩在80分以上(含80分)为优秀,则优秀率不低于多少?
相关知识点
推荐套卷
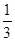 AB,AF=
AB,AF=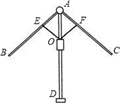
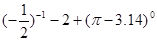

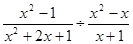
 ;
; 第①步
第①步 .
.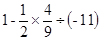 第①步
第①步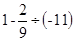 第②步
第②步 第③步
第③步 第④步
第④步

 粤公网安备 44130202000953号
粤公网安备 44130202000953号