已知抛物线的顶点是C (0,a) (a>0,a为常数),并经过点(2a,2a),点D(0,2a)为一定点.
(1)求含有常数a的抛物线的解析式;
(2)设点P是抛物线任意一点,过P作PH⊥x轴,垂足是H,求证:PD = PH;
(3)设过原点O的直线l与抛物线在第一象限相交于A、B两点,若DA=2DB,且S△ABD = 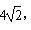 ,求a的值.
,求a的值.
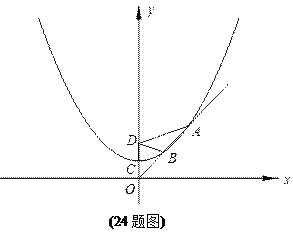
已知抛物线的顶点是C (0,a) (a>0,a为常数),并经过点(2a,2a),点D(0,2a)为一定点.
(1)求含有常数a的抛物线的解析式;
(2)设点P是抛物线任意一点,过P作PH⊥x轴,垂足是H,求证:PD = PH;
(3)设过原点O的直线l与抛物线在第一象限相交于A、B两点,若DA=2DB,且S△ABD = 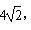 ,求a的值.
,求a的值.
