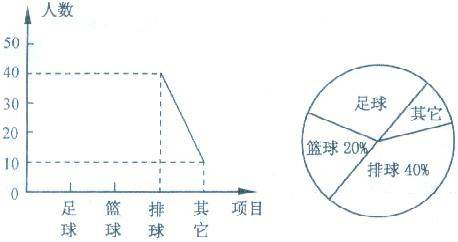
某中学为了解本校学生对球类运动的爱好情况，采用抽样的方法，从足球、篮球、排球、其它等四个方面调查了若干名学生，并绘制成“折线统计图”与“扇形统计图”．请你根据图中提供的部分信息解答下列问题：
（1）在这次调查活动中，一共调查了　　名学生；
（2）“足球”所在扇形的圆心角是　　度；
（3）补全折线统计图．