.在一次课题设计活动中,小明对修建一座87m长的水库大坝提出了以下方案;大坝的横截面为等腰梯形,如图,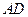 ∥
∥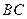 ,坝高10m,迎水坡面
,坝高10m,迎水坡面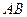 的坡度
的坡度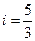 ,老师看后,从力学的角度对此方案提出了建议,小明决定在原方案的基础上,将迎水坡面
,老师看后,从力学的角度对此方案提出了建议,小明决定在原方案的基础上,将迎水坡面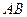 的坡度进行修改,修改后的迎水坡面
的坡度进行修改,修改后的迎水坡面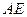 的坡度
的坡度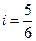 。
。
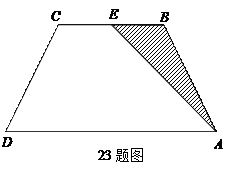
(1) 求原方案中此大坝迎水坡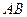 的长(结果保留根号)
的长(结果保留根号)
(2) 如果方案修改前后,修建大坝所需土石方总体积不变,在方案修改后,若坝顶沿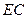 方向拓宽2.7m,求坝顶将会沿
方向拓宽2.7m,求坝顶将会沿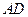 方向加宽多少米?
方向加宽多少米?
.在一次课题设计活动中,小明对修建一座87m长的水库大坝提出了以下方案;大坝的横截面为等腰梯形,如图,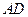 ∥
∥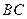 ,坝高10m,迎水坡面
,坝高10m,迎水坡面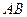 的坡度
的坡度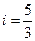 ,老师看后,从力学的角度对此方案提出了建议,小明决定在原方案的基础上,将迎水坡面
,老师看后,从力学的角度对此方案提出了建议,小明决定在原方案的基础上,将迎水坡面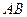 的坡度进行修改,修改后的迎水坡面
的坡度进行修改,修改后的迎水坡面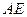 的坡度
的坡度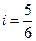 。
。

(1) 求原方案中此大坝迎水坡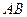 的长(结果保留根号)
的长(结果保留根号)
(2) 如果方案修改前后,修建大坝所需土石方总体积不变,在方案修改后,若坝顶沿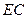 方向拓宽2.7m,求坝顶将会沿
方向拓宽2.7m,求坝顶将会沿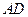 方向加宽多少米?
方向加宽多少米?