已知：AB是⊙O的直径，弦CD⊥AB于点G，E是直线AB上一动点（不与点A、B、G重合），直线DE交⊙O于点F，直线CF交直线AB于点P.设⊙O的半径为r.
（1）如图1，当点E在直径AB上时，试证明：OE·OP＝r2
（2）当点E在AB（或BA）的延长线上时，以如图2点E的位置为例，请你画出符合题意的图形，标注上字母，（1）中的结论是否成立？请说明理由.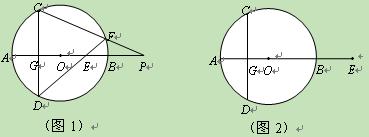
；
大卡的能量，若每人每年要消耗
大卡的植物能量，试问地球能养活多少人？
.
；
；相关知识点
推荐套卷
已知：AB是⊙O的直径，弦CD⊥AB于点G，E是直线AB上一动点（不与点A、B、G重合），直线DE交⊙O于点F，直线CF交直线AB于点P.设⊙O的半径为r.
（1）如图1，当点E在直径AB上时，试证明：OE·OP＝r2
（2）当点E在AB（或BA）的延长线上时，以如图2点E的位置为例，请你画出符合题意的图形，标注上字母，（1）中的结论是否成立？请说明理由.
粤公网安备 44130202000953号